コムドットとは何か？ 中学生でもわかるコムドットのイメージ

参考銘柄Ⅰ（2022,10,04) 1971 中央ビルト 2053 中部飼料 3467 アグレ都市 4428 シノプス 5958 三洋工業 6048 デザインワン 7186 コンコルディア 7578 ニチリョク 8101 GSIクレオス 8584 ジャックス

微分とは何か？ － 中学生でも分かる微分のイメージ

1. Sci-pursuit
2. 数学
3. 微分とは何か？ － 中学生でも分かる微分のイメージ

微分とはズバリ、ある関数の各点における傾き（変化の割合）のことです。

と、いきなり言われてもよくわからないでしょう。そこで、このページでは、中学校で学習した y=ax² のグラフを用いて、中学生でも分かりやすく、微分のイメージを持ってもらえるように微分の解説をします。

微分は科学分野において非常に大事な概念ですので、ぜひ意味を理解してくださいね。やや数学的厳密さを欠いた説明になりますが、それは高校生になってからしっかり学習することにしましょう。

メルボルンは夏時間が始まりましたね。　今朝の気温が6度とまだまだ寒いですが、日が長くなるのが嬉しいですね。

---

もくじ

1. 微分とは
2. 微分はグラフの拡大と同じ
3. y=ax² の x=1 における微分
4. y=ax² の微分
5. 微分を表現する記号

微分とは

いきなりですが、問題です。下のグラフは y=x² のグラフを x=0.5 付近で拡大したものです。

x=0.5 付近のグラフについて、

1. オレンジ色の線はどんな図形に見えますか？
2. その傾きはいくつですか？

y=x² の x=0.5 付近の拡大図

みなさんの答えはどうでしょうか？

1. オレンジ色の線は（ほぼ）直線に見える。
2. 傾きは（ほぼ） 1 である（x が1目盛り増加すると、yがほぼ1目盛り増加している）。

ということでよろしいでしょうか？

さて、これで皆さんはもう、 y=x² を x=0.5 にて微分してしまいました。その値は1なのです。

コムドット　せいら　おっどタクシー

このように、ある（滑らかな）関数を拡大して見たとき、その関数はほぼ直線に見え、一定の傾きを得ることができます。そして、この傾きを求める操作を、ズバリ「微分」というのです。

微分とは何か…？ここではまだ、正確な説明にはなっていませんが、なんとなくイメージを持っていただけたでしょうか？それほど難しいお話しではないですね。

続いては、微分の概念をさらに深めるために、グラフを x=0.5 以外の点でも拡大して傾きを調べ、x の値とその時の傾きの関係を調べてみましょう。

bit-traders.hateblo.jp

微分はグラフの拡大と同じ

微分の説明の前に、傾き＝変化の割合 の復習をしておきましょう。これは中学1年生で学習していますね。

変化の割合とは、 $$\text{変化の割合}=\frac{\text{yの増加量}}{\text{xの増加量}}$$

のことでした。

中学1年生で学習した比例のグラフ y=2x の傾き（=変化の割合）はいくつでしょうか。

y=2xのグラフ

このグラフは、x が1目盛り増加すると、y は2目盛り増加しています。つまり、このグラフの傾き（＝変化の割合）は2ですね。そして、これは x の場所によらず、常に一定です（つまり y=2x を微分すると、2 ということになります…）。

続いて、中学3年で学習する、y=x²のグラフを見てみましょう。

y=x²のグラフ

例として、関数 y=x² にて、x が 2 から 3 まで増加するときの変化の割合を求めてみましょう。

$$\begin{array}{cc}\text{変化の割合}& =\frac{3^2-2^2}{3-2}\\ & =5\end{array}$$

となりますね。

y=x² のグラフに関しては、変化の割合は常に一定ではなく、グラフ上に取る2点の場所によって異なります。

しかし、常に変化の割合（= 傾き）が一定ではない曲線も、ある点でひたすら拡大すると、直線に見えるようになります。

下に、y=x² のグラフを用意しました。線が非常に細く、目盛りも細かいのですが、このグラフは拡大しても画質が落ちないようになっています。これから一緒に、このグラフを拡大して見ていきましょう！

まずは、y=x² 上の x=0.5 の点を拡大してみてみましょう！先ほど拡大図をお見せして確認した通り、その点でのグラフの様子と、傾きを再度調べてください。

y=x² のグラフ（拡大して見てね！）

ところで拡大の方法ですが、スマホでご覧になっている方は、2本指で画面をピンチアウトすることで拡大できます。PC でご覧の方は、グラフをクリックすると、グラフのPDFファイルが開きますので、 を押して拡大してみてください。

さて、そうすると、次のように見えると思います。

y=x² の x=0.5 付近の拡大図

先ほど、「微分とは」の項目でも説明しましたが、再度、次の2点について一緒に確認しましょう。

• 曲線である y=x² のグラフを部分的に拡大すると、それは直線に見える。
• x=0.5 付近での y=x² の傾きはだいたい 1 くらいである。

まず、1点目の「曲線のグラフを拡大すると、直線に見える」ことから。上のグラフを見てみると、オレンジ色の線はやや曲がってはいるものの、直線に近いことが分かると思います。では、もっと拡大してみましょう。下のグラフの1目盛りは、上のグラフと同じです。

y=x² の x=0.5 付近のより詳細な拡大図（一目盛りは上と同じく、1/6）

パッと見では、直線にしか見えませんね。グリッドをよく見ると曲がっているのが分かる程度です。

続いて2点目「x=0.5 付近での y=x² の傾きはだいたい 1 くらいである」ことを確認します。これは、上のグラフを見ると、オレンジの線は x が1目盛り増加すると、y が1目盛り増加しています。すなわち、x=0.5 付近での y=x² の傾き（＝変化の割合）は、$\frac{1}{1}=1$

ということになります。

ここまで理解できましたら、続いては、y=x² のグラフを他の点の付近でも拡大してみましょう。拡大したら直線に見えることを確認し、その直線の傾きを求めていきます。

x=1, 1.5, 2 の点付近で、それぞれ拡大します。

x=1 付近で拡大

y=x² の x=1 付近の拡大図

やはり直線に近いですね。そして、x=1 付近における傾きは、x が1目盛り増加すると、y は2目盛り増加していることが分かるので、$\frac{2}{1}=2$

ということになります。

x=1.5 付近で拡大

y=x² の x=1.5 付近の拡大図

これも直線に近いですね。x=1.5 付近における傾きは、x が1目盛り増加すると、y は3目盛り増加していることが分かるので、$\frac{3}{1}=3$

ということになります。

x=2 付近で拡大

y=x² の x=2 付近の拡大図

これも直線に近く、x=2 付近における傾きは、x が1目盛り増加すると、y は4目盛り増加していることとから、$\frac{4}{1}=4$

ということになります。

さて、これまでの関係をまとめます。

y=x² の x の値に対する近傍での傾き

x	0.5	1	1.5	2
(近傍での) 傾き	1	2	3	4

なんと綺麗な！

これまでの結果より、y=x² 上のある点における傾きは、その点の x 座標の2倍という関係が得られました。たかが4つの点からの推測に過ぎませんが、これが本当に成り立つとすれば、非常に興味深い関係ですね。

実は！この関係は、すべての点に成り立つことが、この後の証明で分かります。つまり、y=x² の各点における傾きは、各点の x 座標に対して 2x と表すことが出来ます。これが、x=0 のときでも、x が負のときでも成り立つのです。

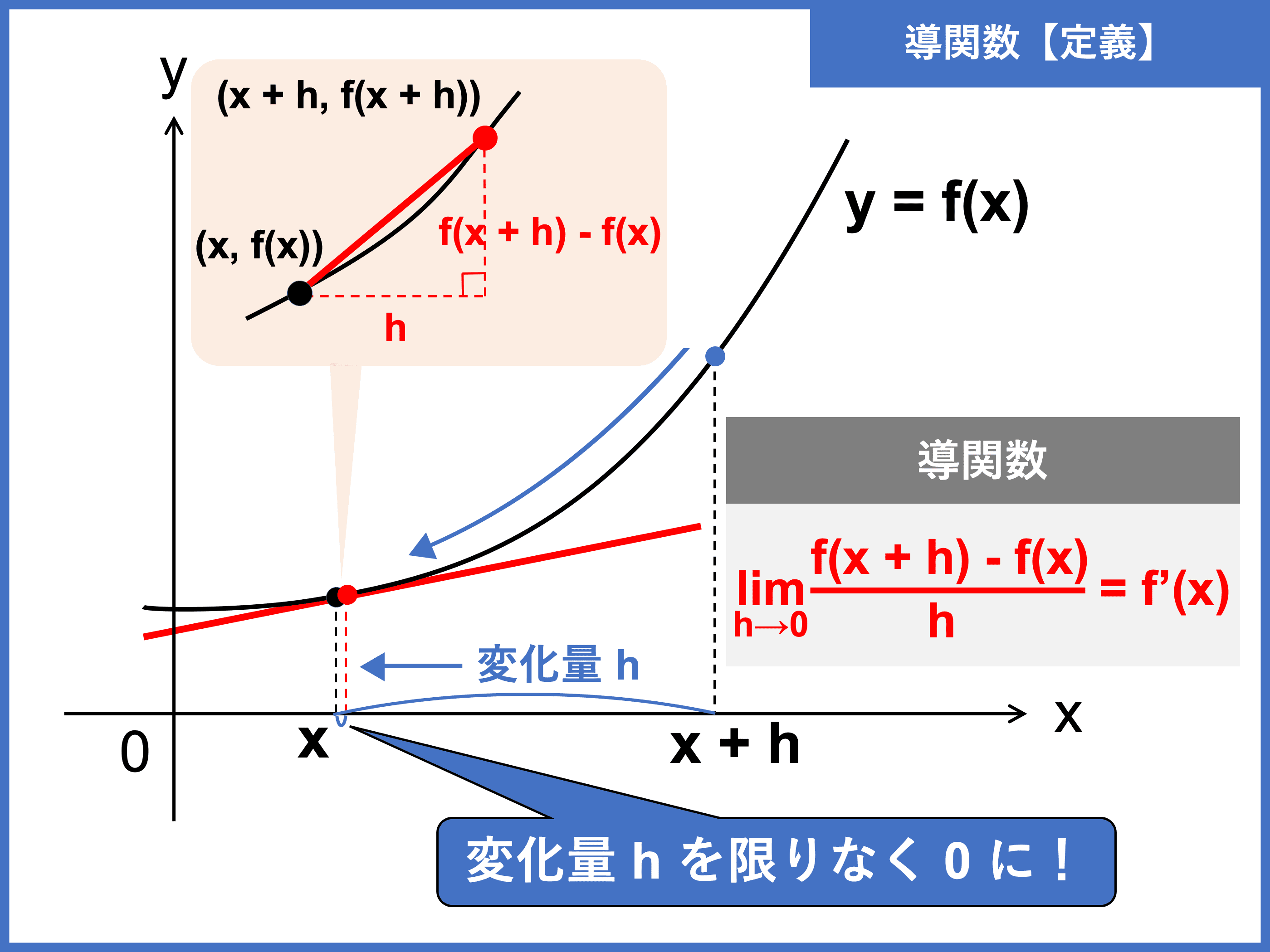
このように、ある関数（今の場合は、y=x²）の任意の点における傾きを導く式を導関数といい、この導関数を求めることを、一般に微分というのです。

さて、これまでの話はグラフの見た目に頼った話で、「ほぼ直線」とか「傾きがほぼ１」というように「ほぼ」という言葉が微妙で、数学らしくなかったですね。続いては、数式を使って微分の説明をします。中学生でも分かるように、丁寧に解説していきますので、ぜひ続けて読んでくださいね。

 

y=x² の x=1 における微分

ここまでのお話しで、微分の概念については理解していただけたと思います。

これまでの話は、グラフの「見た目」に頼った感覚的な理解だったので、ここからは、式を使った、数学的な理解をしてみましょう。

y=x² の x=1 における傾きが 2 である、というお話しをしましたが、果たして本当にそういえるのか？を確認してみます。

まずは x=1 の点と、その近くの点の2点間の変化の割合を、具体的に求めてみます。

たとえば、y=x² において x=1.0 から x=1.1 まで増加するときの変化の割合は $$\begin{array}{cc}\text{変化の割合}& =\frac{\text{yの増加量}}{\text{xの増加量}}\\ & =\frac{{1.1}^2-{1.0}^2}{1.1-1.0}\\ & =\frac{0.21}{0.1}\\ & =2.1\end{array}$$

となります。つまり、y=x² 上の x=1.0 の点と x=1.1 の点の2点を通る直線の傾きは、2.1 だということになります。

さて、続けて、x=1 にもっと近い点を取って、変化の割合を求めてみましょう。今求めたいのは、x=1 付近を限りなく拡大した時の傾きですから、それは x=1 により近い2点間の変化の割合を求めることに対応します。

y=x² において x=1.00 から、x=1.01 まで増加するときの変化の割合を計算します。

$$\begin{array}{cc}\text{変化の割合}& =\frac{\text{yの増加量}}{\text{xの増加量}}\\ & =\frac{{1.01}^2-{1.0}^2}{1.01-1.0}\\ & =\frac{0.0201}{0.01}\\ & =2.01\end{array}$$

となります。つまり、y=x² 上の x=1.00 の点と x=1.01 の点の2点を通る直線の傾きは、2.01 だということになります。先ほどの 2.1 という結果よりも、2 に近づきましたね。

このように、x=1 における傾きを求めるには、y=x² 上の x=1 の点の他に、もう1点別の点を取り、この2点間の変化の割合を求めるという方法を使います。

今は、2点間の距離（これを h としましょう）が、h = 1.1 - 1.0 = 0.1 のときと、h = 1.01 - 1.00 = 0.01 のときの2種類を実際に代入してみました。この h を小さくすると、予想していた値 2 により近づきましたね。では、もっともっと2点間の距離 h を小さくしたら、どのようになるでしょうか。予想通り、2 といえるのでしょうか。文字式を使って計算してみましょう。

これまでと同様の手順で、x=1 の点と、そこから x の距離が h 離れた x=1+h の点、この2点間の変化の割合を求めましょう。

$$\begin{array}{cc}\text{変化の割合}& =\frac{\text{yの増加量}}{\text{xの増加量}}\\ & =\frac{(1+h{)}^2-1^2}{(1+h)-1}\\ & =\frac{(1+2h+h^2)-1}{(1+h)-1}\\ & =\frac{2h+h^2}{h}\\ & =2+h\end{array}$$

という関係式が得られました。この式を使うと、先ほど求めた、x=1 と x=1.1 のときの変化の割合は、h = 1.1 - 1 = 0.1 より、2 + h = 2.1 と、簡単に求めることが出来ます。x=1 と x=1.01 の2点間での変化の割合も同様にして、求められます。

さて、では2点間の距離 h を限りなく 0 に近づけていったとき、その変化の割合はどうなるでしょうか？それは、先ほどの 2 + h にて h を 0 にしたときの値、つまり 2 ですね。したがって、y=x² の x=1 における傾きは、2 であることが証明できました。

 

y=x² の微分

上では、関数 y=x² の x=1 の点での傾きを計算で求め、証明しました。今度は、x=1 以外のすべての点における傾きを、計算によって求めてみましょう。先に、グラフを「見て」予想した結果からは、 y=x² 上の各 x の点における傾きは、2x となるはずです。

x=1 の点における傾きを計算で求めたように、今度は一般の x の点における傾きを求めます。この点から h だけ離れた点との、2点間における変化の割合は、

$$\begin{array}{cc}\text{変化の割合}& =\frac{\text{yの増加量}}{\text{xの増加量}}\\ & =\frac{(x+h{)}^2-x^2}{(x+h)-x}\\ & =\frac{(x^2+2hx+h^2)-x^2}{(x+h)-x}\\ & =\frac{2hx+h^2}{h}\\ & =2x+h\end{array}$$

となります。x=1 を代入すると、先ほどの 2+h という式と同じになりますね。

2点間の x 座標の距離 h を限りなく 0 にすると、この式は 2x となります。したがって、関数 y=x² の各 x に対して、その点における傾きは 2x となります。これで、このページの最初に、グラフを拡大して予想した結果と、計算結果が一致したことを確認できました。

すなわち、関数 y=x² を微分した値は、2x ということを証明できました。

※本当はもうちょっとだけ正確な議論が必要なのですが、それは高校生になってから確認するとしましょう。

微分を表現する記号

最後に、微分を記述するための記号を紹介します。これは高校で学習してから使えればいいのですが、Wikipedia などに掲載されている理系の記事を見ているとよく登場する記号なので、ちょっと知っておくといいかもしれません。

まず、関数 $y=x^2$

を微分して得られた導関数を $y^{\prime }=2x$ と書きます。ここで、$y^{\prime }$ は「yダッシュ」や「yプライム」と読みます。このプライム記号が、微分した導関数であることを示します。また、別の書き方では、 $$\frac{dy}{dx}=\frac{d}{dx}{x}^2=2x$$ のようにも書きます。関数の前に、$$\frac{d}{dx}$$

という記号を付けることで、その関数を x で微分するということを示します。

$d$

というのは何か…というと、差分を表す Δ（デルタ、delta）の d ではないかと思います。もしくは、微分の英語読み differential の d かもしれません。

また、y=x² を微分する過程で、x の変化量 h を限りなく 0 に近づけるという表現をしました。これは、極限の記号 $lim$

の下に $h\to 0$

と書くことで表します。つまり、次のように書き表します。

$$\begin{array}{cc}& \underset{h\to 0}{lim}\frac{(x+h{)}^2-x^2}{(x+h)-x}\\ & =\underset{h\to 0}{lim}(2x+h)\\ & =2x\end{array}$$

または $$\begin{array}{cc}& \frac{(x+h{)}^2-x^2}{(x+h)-x}\\ & =2x+h\\ & \underset{h\to 0}{\overset{}{\to }}2x\end{array}$$

$lim$

は「リミット」とよみ、極限（limit）を取る記号です。

• 微分とは？
  • 微分の記号
• 微分のやり方
  • ① 導関数の定義に従って微分する
  • ② 微分公式を使って微分する
• 微分の基本公式一覧（数II）
  • 定数倍の微分
  • 和と差の微分
  • べき乗の微分
  • 定数の微分
• 微分の応用公式一覧（数III）
  • 三角関数の微分
  • 指数関数の微分
  • 対数関数の微分
  • 積の微分
  • 商の微分
  • 合成関数の微分
  • 対数微分法

微分とは？

微分とは、ある関数 f(x) の導関数 f′(x) を求める演算のことです。

さて、では導関数って何？と思いますよね。

導関数とは、関数 y=f(x) のある点における瞬間の変化率（すなわち接線の傾き）を求められる関数で、次のように定義されます。

導関数の定義

関数コムドットやまと の導関数コムドットひゅうが は

f′(x)=limh→0f(x+h)−f(x)h

合わせて読みたいコムドットあむぎり

「せいらViVi専属モデル導関数」については、以下の記事で詳しく説明しています。

この記事を学習する前に理解しておくことをオススメします！

導関数と微分係数の違いとは？定義・公式・求め方を解説！

モデルプレス微分の記号

メリット：微分することは、元の関数に「′」をつけて表すことが多いです。

微分の記号①

関数コムドットやまと yアイドル=f(x) を x についてアイドル2.0で微分することを次のように表す。

f′(x)コムレンジャーまたは 中学生y′

（例）

• y=x2+2x+3 アイドル2.0を微分
  → (x2+2x+3)′ または y′
• y=3x3+1 を微分
  → (3x3+1)′ または y′

ただし、「′コムレンジャーin韓国　」で表すと、関数を何で微分するのかがあいまいになってしまいます。

そこで、対象を明確にした次のような表記を使うこともあります。

微分の記号②

関数 y=f(x) コムドットゆうたを x 那須ほほみについて微分することを次のように表す。

dydx または ddxf(x)

分数のようなかたちで、「分子の関数を分母の変数で微分する」ことを表しています。

これで、何についての微分なのかが簡単に表現できます。

（例）

• y=g(x) を x について微分
  → dydx または ddxg(x)
• x=2t2+t−1 を t について微分
  → dxdt

問題の中で微分する対象が明確な場合は「′」による表記で大丈夫です！

微分のやり方

微分には、「① 導関数の定義に従ったやり方」と「② 微分公式を利用するやり方」があります。

① 導関数の定義に従って微分する

まずは導関数の定義に従った微分のやり方です。

例題

次の関数を微分せよ。

y=x2−3x+9

導関数の定義式 f′(x)=limh→0f(x+h)−f(x)h に問題の関数を当てはめて、導関数 y′ を求めます。

解答

y=f(x) とおくと、

y′=limh→0f(x+h)−f(x)h

f(x+h)−f(x)

={(x+h)2−3(x+h)+9} − (x2−3x+9)

=(x2+2hx+h2−3x−3h+9) − x2+3x−9

=2hx+h2−3h

=h(2x+h−3)

よって、

y′=limh→0h(2x+h−3)h=limh→0(2x+h−3)=2x−3

答え：　y′=2x−3

これが、導関数の定義に従った微分のやり方です。

しかし、関数を微分するたびに定義どおりの計算を行うのは大変ですよね。

そこで、次に示すやり方②のように微分の法則性をまとめた公式を使うことで、計算を省略することができます。

② 微分公式を使って微分する

次に、微分公式を使った微分のやり方です。

例題

次の関数を微分せよ。

y=x2−3x+9

先ほどと同じ例題ですが、微分公式を使うと一瞬で答えにたどり着けます。

なお、この問題で使う微分公式はかっこ書きのリンクから確認できます。

解答

y′=(x2−3x+9)′

=(x2)′−(3x)′+(9)′（和と差の微分）

=(x2)′−3(x)′+(9)′ （定数倍の微分）

=2x−3⋅1+0 （べき乗の微分、定数の微分）

=2x−3 

答え：　y′=2x−3

以降、高校で習うすべての微分公式を、数IIで習う基本公式と数IIIで習う応用公式に分けて説明していきます。

 

微分の基本公式一覧（数II）

ここでは、主に数IIで習う基本的な微分公式を解説します。

補足

以降、f(x), g(x) を x の関数とし、α, β を定数として公式を示していきます。

定数倍の微分

関数に定数倍の係数がかかっている場合は、係数を微分の外に出すことができます。

定数倍の微分

(αf(x))′=αf′(x)

（例）

• (3x)′=3(x)′
• (−5x2)′=−5(x2)′
• {12(x3+5x−1)}′ =12(x3+5x−1)′

和と差の微分

複数の関数の和や差で表された式は、個々の関数に分けて微分できます。

和と差の微分

• (f(x)+g(x))′=f′(x)+g′(x)
• (f(x)−g(x))′=f′(x)−g′(x)
• (αf(x)+βg(x))′=αf′(x)+βg′(x)
• (αf(x)−βg(x))′=αf′(x)−βg′(x)

つまり、多項式を微分する場合は項ごとに微分できるということですね。

（例）

• (x2−3x+9)′=(x2)′−3(x)′+(9)′
• (2x3+5x−3)′ =2(x3)′+5(x)′−(3)′

べき乗の微分

べき乗 xn の関数は、次のように微分できます。

べき乗の微分公式

n が自然数のとき、

(xn)′=nxn−1

※ なお、p が有理数であっても、

(xp)′=pxp−1

が成り立つ。

べき乗の項を微分するときは、指数を係数として前に下ろし、指数は 1 を引けばよいのですね。

（例）

• (x)′=(x1)′=1x0=1
• (x2)′=2x1=2x
• (x43)′=43x43−1=43x13
• (x−4)′=(−4)x−4−1=−4x−5

補足

※ で示したように、指数が分数や負の数であっても公式は成り立ちます。

定数の微分

一方、定数項を微分すると必ず 0 となります。

定数の微分公式

k が実数のとき、

(k)′=0

（例）

• 9)′=0
• (−6)′=0

以上が、微分の基本公式でした。

基本公式の例題はここをクリック

例題「基本公式を使って微分する」

例題

次の関数を微分せよ。

(1) y=4x3−5x2−3x−6

(2) y=(5x+3)(x−2)

(3) y=x−3+x12+1

因数分解されていれば、微分する前に展開しておきます。

微分するときは、個々の項に分けて考えます。べき乗の微分は慣れるまでていねいに計算しましょう。

解答

(1)

y′=(4x3−5x2−3x−6)′=4(x3)′−5(x2)′−3(x)′−(6)′=4⋅3x2−5⋅2x1−3⋅1x0−0=12x2−10x−3

答え：　12x2−10x−3

(2)

(5x+3)(x−2)=5x2−7x−6 より、

y′=(5x2−7x−6)′=5(x2)′−7(x)′−(6)′=5⋅2x−7⋅1−0=10x−7

答え：　10x−7

(3)

y′=(x−3+x12+1)′=(x−3)′+(x12)′+(1)′=−3x−4+12x−12+0=−3x−4+12x−12(=−3x4+12x−−√)

答え：　−3x−4+12x−12 または −3x4+12x−−√

数IIまで勉強する方は、ここまで理解できていれば大丈夫です！

微分の応用公式一覧（数III）

続いて、数IIIで習う微分の応用公式を紹介していきます。

これらの公式を使うと、より複雑な関数の微分が可能になります。

三角関数の微分

まずは三角関数の微分公式です。

三角関数の微分

• (sinx)′=cosx
• (cosx)′=−sinx
• (tanx)′=1cos2x

sinx, cosx, tanx の微分の 3 点セットは必ず暗記しておきましょう！

例題はここをクリック

例題「三角関数を微分する」

例題

次の関数を微分せよ。

y=sinx+cosx−tanx

cosx の微分だけ符号が変わることに注意します。

解答

y′=(sinx)′+(cosx)′−(tanx)′=cosx−sinx−1cos2x

答え：　cosx−sinx−1cos2x

合わせて読みたい

三角比・三角関数を総まとめ！定義・定理・公式一覧

指数関数の微分

続いて、指数関数の微分公式です。

指数関数の微分

a>0, a≠1 のとき、

• (ex)′=ex
• (ax)′=axloga

ex は微分しても式が変わらないことを覚えておきましょう。

例題はここをクリック

例題「指数関数を微分する」

例題

次の関数を微分せよ。

(1) y=−2ex

(2) y=3x

解答

(1) y′=−2(ex)′=−2ex

(2) y′=(3x)′=3xlog3

答え：　(1) −2ex、(2) 3xlog3

合わせて読みたい

指数関数とは？グラフや公式、微分積分をわかりやすく解説

対数関数の微分

対数関数の微分公式は次の通りです。

対数関数の微分

a>0, a≠1 のとき、

• (logx)′=1x
• (logax)′=1xloga
• (log|x|)′=1x
• (loga|x|)′=1xloga

特に (logx)′=1x はよく使うので必ず覚えておきましょう！

補足

底が e の自然対数「logex」は、 e を省略して「logx」と書くことが多いです。

例題はここをクリック

例題「対数関数を微分する」

例題

次の関数を微分せよ。

(1) y=3log|x|

(2) y=2log5x

解答

(1) y′=3(log|x|)′=3x

(2) y′=2(log5x)′=2xlog5

答え：　(1) 3x、(2) 2xlog5

合わせて読みたい

対数関数とは？グラフや公式、微分積分をわかりやすく解説

積の微分

2 つの関数のかけ算で表された関数は、交互に微分して足し合わせてあげます。

積の微分

(f(x)g(x))′=f′(x)g(x)+f(x)g′(x)

例題はここをクリック

例題「べき乗関数と対数関数の積を微分する」

例題

y=x3logx を微分せよ。

関数 x3 と関数 logx がかけ算された積の微分ですね。

解答

y′=(x3)′logx+x3(logx)′=3x2logx+x3⋅1x=3x2logx+x2=x2(3logx+1)

答え：　x2(3logx+1)

商の微分

関数同士の割り算で表された関数は、分母を 2 乗し、分子に「(分子の微分)(分母)−(分子)(分母の微分)」をもってきます。

商の微分

(f(x)g(x))′=f′(x)g(x)−f(x)g′(x){g(x)}2

特に f(x)=1 のとき

(1g(x))′=−g′(x){g(x)}2

少し覚えづらいですが、問題をたくさん解いて頭に叩き込みましょう。

例題はここをクリック

例題「分数関数を微分する」

例題

y=x2+x−1x2+1 を微分せよ。

関数が関数で割られているので、商の微分が使えますね。

解答

（見切れる場合は横へスクロール）

y′

=(x2+x−1)′(x2+1)−(x2+x−1)(x2+1)′(x2+1)2

=(2x+1)(x2+1)−(x2+x−1)2x(x2+1)2

=(2x3+2x+x2+1)−(2x3+2x2−2x)(x2+1)2

=−x2+4x+1(x2+1)2

=−x2−4x−1(x2+1)2

答え：　−x2−4x−1(x2+1)2

合わせて読みたい

分数関数とは？グラフの書き方、分数不等式、微分積分を解説

合成関数の微分

続いて、2 つの関数が合成された関数の微分方法です。

合成関数の微分

y が u の関数で、u が x の関数であるとき、y を x について微分すると

dydx=dydu⋅dudx

y=f(u), u=g(x) とおくと

y′={f(g(x))}′=f′(g(x))g′(x)

u=g(x) を箱とみて、「(全体を箱について微分)×(箱の中身を微分)」をすると覚えておきましょう。

例題はここをクリック

例題①「因数分解された関数を微分する」

例題①

y=(x2−2)3 を微分せよ。

このまま解こうと思うと、右辺を展開する必要があります。

ここで、括弧の中身 x2−2 を 1 つの箱 □ と見ると、

• y=□3
• □=x2−2

という 2 つの関数が合成されていると見ることができます。

この合成関数を x について微分すると、

y′=(□3)′□′

と計算できます。

実際にやってみましょう。

解答

y=(x2−2)3 を微分すると、

y′=3(x2−2)2⋅(x2−2)′=3(x2−2)2⋅2x=6x(x2−2)2

答え：　6x(x2−2)2

Tips

全体を □ について微分するときは、□ を単なる変数と見ることがポイントです。

もう 1 問、合成関数の問題を見てみましょう。

例題②「3 つの関数が合成された関数を微分する」

例題②

y=log(sin2x)

今度は、対数関数 log□ と三角関数 □=sin2x が合成されていますね。

また、sin2x も □=△2 と △=sinx が合成されているので、二重に合成されていることになります。

y′=(log□)′□′=(log□)′2△△′

それでは解答です。

解答

y=log(sin2x)

y′=1sin2x⋅2sinx⋅cosx=2cosxsinx

答え：　2cosxsinx

いかがでしたか？

合成関数の微分は間違えやすいので、たくさん練習を積んでコツをつかんでいきましょう。

合わせて読みたい

合成関数とは？意味や公式、微分積分をわかりやすく解説

対数微分法

対数微分法とは、両辺の対数をとってから微分する方法で、累乗の積や商で表された関数を微分するときに便利です。

対数微分法

y=f(x) を対数微分法で微分する手順は次のとおりである。

1. y=f(x) の両辺の絶対値の自然対数をとる（ただし、y=f(x)≠0 ）
   log|y|=log|f(x)|

2. 両辺を x で微分する
   合成関数の微分の考え方から
   (ddylog|y|)dydx =(ddf(x)log|f(x)|)ddxf(x)
   よって、1ydydx=1f(x)f′(x)

3. 左辺が dydx （求めたい導関数）だけになるように式変形する
   両辺に y をかけて
   dydx=yf(x)f′(x)
   y=f(x) より yf(x)=1 であるから、
   dydx=f′(x)

補足

最初に両辺の絶対値の自然対数をとるのは、真数条件（真数 >0）を満たすためです。

あらかじめ両辺が正の数とわかっている場合は、絶対値は必要ありません。

また、とるのは必ず底が e の「自然対数」です。

 

微分公式は以上です！

微分は入試でも頻出の単元なので、苦手なままだとかなり痛いです。

とにかくたくさん問題を解いて、公式ややり方をマスターしていきましょう！